Quelles influences peut avoir un substrat sec ou liquide sur la dynamique et la forme d’une bulle baignée dans un champ électrique ? Une question sur laquelle se sont penchés les chercheurs du GRASP, le Groupe de recherche et d'applications en physique statistique de l’ULiège, avec une meilleure compréhension de la dynamique des bulles et de leur ménisque sous champs électriques viennent d’être publiés dans la revue Physical Review Fluids.
Une des capacités les plus remarquables de la bulle est de spontanément adopter, une fois soufflée, la forme d'une sphère parfaite. Cette propriété est liée à sa structure très particulière qui met en jeu deux échelles de grandeur fortement différentes. En effet, la bulle est un objet centimétrique qui est composé d'une fine membrane savonneuse dont l'épaisseur ne dépasse généralement pas le micromètre. C'est grâce à cette très fine membrane liquide, qui sépare l'air encapsulé de celui de l'extérieur, que l'on peut observer de superbes couleurs sur une bulle sphérique flottant au vent.
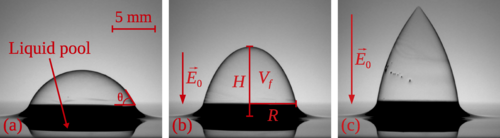
C'est d'ailleurs la présence de cette membrane, et donc de deux interfaces air-liquide, qui permet de distinguer les bulles des gouttes. En effet, ces dernières ne possèdent qu'une seule et unique interface, ce qui fait que le volume d’une goutte est entièrement composé de liquide, et est donc plus « lourd » que celui d’une bulle. De ce fait, les gouttes sont plus sensibles à la gravité et se déforment beaucoup plus sous ses effets que les bulles. « Il est toutefois possible de modifier la forme d'une bulle d'autres manières, comme par exemples avec des champs électriques, explique Sébastien Mawet, doctorant au GRASP (Unité de recherches CESAM/Faculté des Sciences) de l’ULiège et premier auteur de l’article publié dans Physical Review Fluids. En effet, une fois déposée sur un substrat pour faciliter son étude et baignée dans un champ électrique, la bulle initialement hémisphérique se déforme en une demi-ellipse et adopte la forme d'un demi-ballon de rugby. « Si l'on continue à augmenter le champ jusqu'à atteindre des valeurs de l'ordre de plusieurs kilovolts par millimètre, reprend Sébastien Mawet, la bulle change encore une fois de forme pour adopter celle d'un cône. Une fois dans cet état, la bulle se met à éjecter à très grande vitesse des gouttelettes chargées micrométriques depuis sa pointe. » Ce phénomène physique porte le nom de « cône de Taylor », en mémoire du premier chercheur à lui avoir donné une explication.
« Ce phénomène est particulièrement étudié sur les gouttes, explique Stéphane Dorbolo, Chercheur qualifié FNRS au GRASP et co-auteur de l’étude, car il est à la base des techniques d'électrosprays et d'électrofilages qui trouvent leurs utilités dans des domaines variés allant de l'imprimerie de très haute résolution à la propulsion spatiale, en passant par la création de pansements de nanofibres permettant de dispenser très efficacement des médicaments directement sur une plaie. » Cependant, dans chacune de ces technologies, les gouttes reposent sur des substrats solides et non liquides. En effet, les techniques nécessaires à l'étude d'une goutte sur son propre liquides sont difficiles à mettre en place.
Une des capacités les plus remarquables de la bulle est de spontanément adopter, une fois soufflée, la forme d'une sphère parfaite. Cette propriété est liée à sa structure très particulière qui met en jeu deux échelles de grandeur fortement différentes. En effet, la bulle est un objet centimétrique qui est composé d'une fine membrane savonneuse dont l'épaisseur ne dépasse généralement pas le micromètre. C'est grâce à cette très fine membrane liquide, qui sépare l'air encapsulé de celui de l'extérieur, que l'on peut observer de superbes couleurs sur une bulle sphérique flottant au vent.
C'est d'ailleurs la présence de cette membrane, et donc de deux interfaces air-liquide, qui permet de distinguer les bulles des gouttes. En effet, ces dernières ne possèdent qu'une seule et unique interface, ce qui fait que le volume d’une goutte est entièrement composé de liquide, et est donc plus « lourd » que celui d’une bulle. De ce fait, les gouttes sont plus sensibles à la gravité et se déforment beaucoup plus sous ses effets que les bulles. « Il est toutefois possible de modifier la forme d'une bulle d'autres manières, comme par exemples avec des champs électriques, explique Sébastien Mawet, doctorant au GRASP (Unité de recherches CESAM/Faculté des Sciences) de l’ULiège et premier auteur de l’article publié dans Physical Review Fluids. En effet, une fois déposée sur un substrat pour faciliter son étude et baignée dans un champ électrique, la bulle initialement hémisphérique se déforme en une demi-ellipse et adopte la forme d'un demi-ballon de rugby. « Si l'on continue à augmenter le champ jusqu'à atteindre des valeurs de l'ordre de plusieurs kilovolts par millimètre, reprend Sébastien Mawet, la bulle change encore une fois de forme pour adopter celle d'un cône. Une fois dans cet état, la bulle se met à éjecter à très grande vitesse des gouttelettes chargées micrométriques depuis sa pointe. » Ce phénomène physique porte le nom de « cône de Taylor », en mémoire du premier chercheur à lui avoir donné une explication.
« Ce phénomène est particulièrement étudié sur les gouttes, explique Stéphane Dorbolo, Chercheur qualifié FNRS au GRASP et co-auteur de l’étude, car il est à la base des techniques d'électrosprays et d'électrofilages qui trouvent leurs utilités dans des domaines variés allant de l'imprimerie de très haute résolution à la propulsion spatiale, en passant par la création de pansements de nanofibres permettant de dispenser très efficacement des médicaments directement sur une plaie. » Cependant, dans chacune de ces technologies, les gouttes reposent sur des substrats solides et non liquides. En effet, les techniques nécessaires à l'étude d'une goutte sur son propre liquides sont difficiles à mettre en place.
Plus d’infos sur : https://www.grasp.uliege.be/cms/c_7511910/fr/l-influence-du-substrat-sur-la-forme-et-la-dynamique-des-bulles
Article paru dans Physical Review Fluids : https://journals.aps.org/prfluids/abstract/10.1103/PhysRevFluids.6.043603